SMART/REDUCED SYLLABUS
MODEL PAPER OF MATHEMATICS FOR GRADE-9
Objective Type
Time allowed: 20 Minutes. Maximum Marks: 15
Note: Four possible answers A, B, C and D to each question are given. The choice which you think is correct, fill that circle with marker or ink pen in the answer-book. Cutting or filling two or more circles will result in zero mark in that question.
Q.1 (i)
The product of \( (3 + \sqrt{5})(3 - \sqrt{5}) \) is:
(ii)
The base of common logarithm is:
(iii)
If \( A = \{ \} \), then \( P(A) \) is:
(iv)
If \( n(A \cup B) = 50, n(A) = 30 \) and \( n(B) = 35 \), then \( n(A \cap B) = \):
(v)
The LCM of \( 16x^2, 4x \) and \( 30xy \) is:
(vi)
The factorization of \( 12x+36 \) is:
(vii)
Solution of \( 5x - 10 = 10 \) is:
(viii)
\(\sin 60^\circ =\) ______.
(ix)
\(\sec^2 \theta - \tan^2 \theta =\) ______.
(x)
Distance between two points \(P(1, 2)\) and \(Q(4, 6)\) is:
(xi)
If the volume of two similar solids is 125 cm³ and 27 cm³, the ratio of their corresponding heights is:
(xii)
Slope of the line \(y = 5x + 3\) is:
(xiii)
An equilateral triangle ______.
(xiv)
Which data takes only some specific values?
(xv)
While rolling a pair of dice, what will be the probability of double 2?
Subjective Type (Part-I)
Time allowed: 2:10 hrs. Max. Marks: 60
Q.
2: Write short answers to any six (06) questions: (2 × 6 = 12)
(i) Find two rational numbers between 2 and 3.
(ii) Simplify \( \left( \frac{3}{4} \right)^{3/2} \div \left( \frac{4}{9} \right)^{3} \times \frac{16}{27} \).
(iii) Find the value of \( x \) in \(\log_{10} x = -3 \).
(iv) Find characteristic of 0.000049.
(v) Write down the power set of {+, -, ×, ÷}.
(vi) Define difference of two sets.
(vii) Factorize \( x^2 + x - 12 \).
(viii) Factorize \( 125a^2 - 1 \).
(ix) Solve \( 12x + 30 = -6 \) and represent the solution on a real line.
Q.
3: Write short answers to any six (06) questions:
(i) Convert \( 315^\circ \) to radians.
(ii) Find the arc length if \( r = 6 \) cm and central angle \( \theta = \frac{\pi}{3} \) radians.
(iii) Evaluate \( 2 \cos \frac{\pi}{3} \sin \frac{\pi}{3} \).
(iv) Find the distance between the points \( L(0, 3) \) and \( M(-2, -4) \).
(v) Find the slope of the line joining the points \( (3, -2) \) and \( (2, 7) \).
(vi) Find the equation of the horizontal line through \( (7, -9) \).
(vii) Find the unknown in the given figure.
(viii) The radii of two spheres are in the ratio of 3:4. What is the ratio of their volumes?
(ix) The mass of sack of rice is 50 kg and height 60 cm. Find the mass of the similar sack of rice with height of 90 cm.
Q.
4: Write short answers to any six (6) questions:
(i) Sketch the graph of \(y=2x-1\).
(ii) Plot the graph of the function \(y=5^{-x}\).
(iii) Construct a triangle \(BCD\) in which measures of two sides are 5.5 cm and 4.2 cm and measure of their included angle is \(60^{\circ}\).
(iv) Define orthocentre.
(v) Define Arithmetic Mean (AM).
(vi) The marks in mathematics of Jamal in eight monthly tests were 75, 76, 80, 80, 82, 82, 82, 85. Find the mode of the marks.
(vii) Following are the heights in (inches) of 12 students. Find the median height.
55, 53, 54, 58, 60, 61, 62, 56, 57, 52, 51, 63.
(viii) Abdul Raheem rolls a fair dice, what is the probability of getting the number divisible by 3?
(ix) Define sample space.
Subjective Type (Part-II)
Note: Attempt any two questions.
Q. 5:
(a) Simplify the following \(\frac{(25)^{\frac{3}{2}}\times(243)^{\frac{3}{5}}}{(16)^{\frac{5}{4}}\times(8)^{\frac{4}{3}}}\).
(b) Find the value of \(x\).
\(\log x=-2.0184\)
Q.
6:
(a) There are 98 secondary school students in a sports club, 58 students join the swimming club, and 50 join the tug of war club. How many students participated in both games?
(b) Factorize \(x^{4}-30x^{2}y^{2}+9y^{4}\).
Q. 7:
(a) Indicate the solution region of the following linear inequalities by shading:
\(2x-3y\le6;\) \(2x+3y\le12\)
(b) Prove that \((\tan \theta+\cot \theta)^{2}=\sec^{2}\theta \csc^{2}\theta\).
Q. 8:
(a) Show that the points \(A(0,2)\), \(B(\sqrt{3}, 1)\) and \(C(0,-2)\) are vertices of a right triangle.
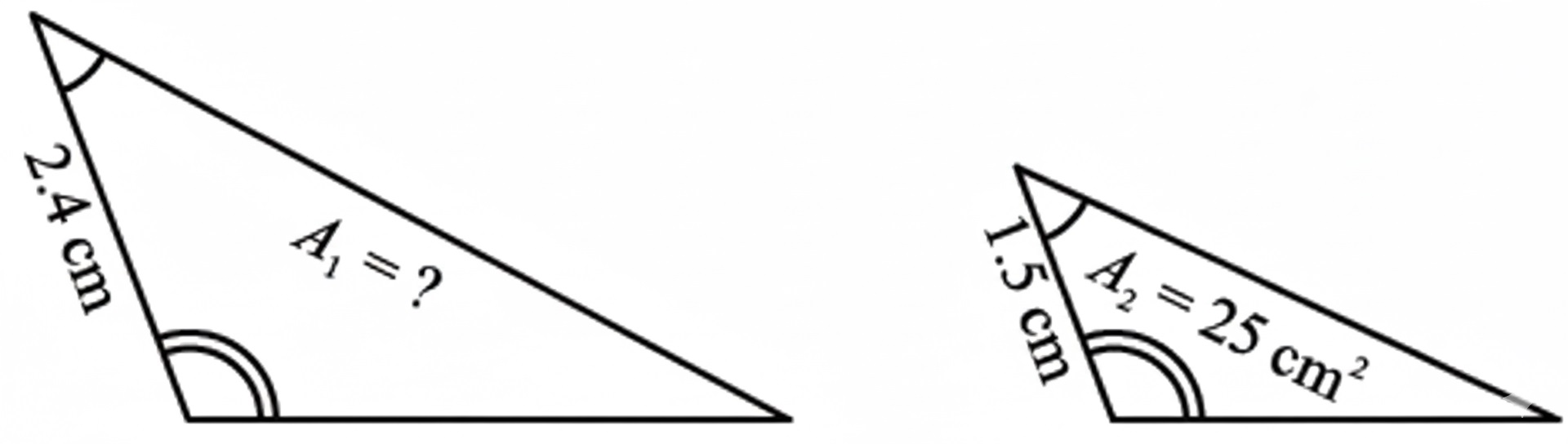
(b) Find the unknown value in the following:
Q. 9:
(a) A set of data contains the values as 148, 145, 160, 157, 156, 160.
Show that Mode > Median > Mean.
(b) The frequency of defective products in 750 samples are shown in the following table. Find the relative frequency for the given table.
| No. of defectives per sample | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| No. of sample | 120 | 140 | 94 | 85 | 105 | 50 | 40 | 66 | 50 |